Finding Paths in Networks #

Pathfinding is a handy method for getting from one point to another, and it’s used in loads of different scenarios where you want to minimise the number of connections without spending too much. This is especially helpful when studying networks, as it helps us uncover important connections between different nodes.

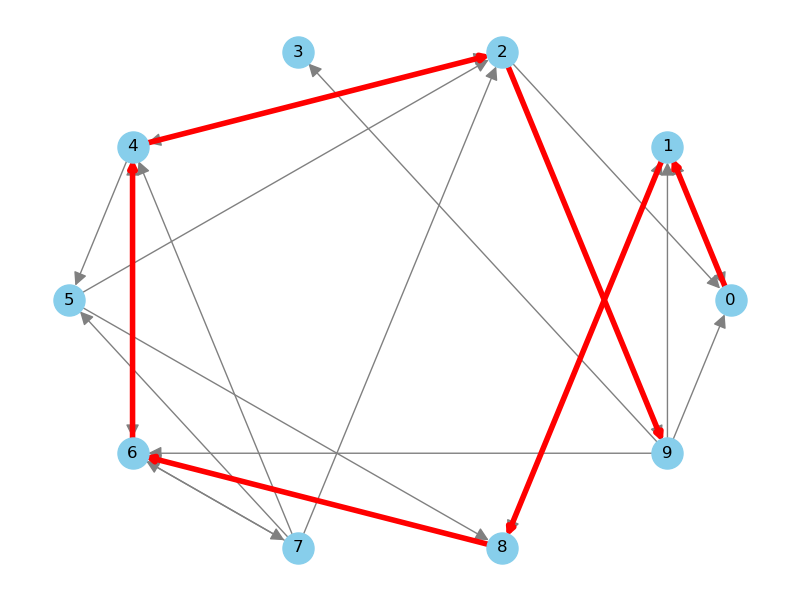
For example, imagine I’ve created a random network and need to go from node 0 back to node 0. The network below shows a potential path to achieve that. In this case, the nodes 0, 1, 8, 6, 4, 2, and 9 form the shortest possible route to reach the destination.

Examples of Pathfinding #

Pathfinding shows up in a bunch of everyday applications. Here are just two examples of where you might come across it.

Games #

From maze-solving to MMORPGs, pathfinding plays a big part. In maze-solving, for instance, the aim is often to guide a character or agent through a virtual space without bumping into walls or other players. Since computers are so efficient at finding paths, game developers sometimes have to make them a bit “dumber” to make things feel more realistic. This can be done by adding a bit of random noise, so it looks like the computer is making small mistakes now and again.

Sat-navs (GPS) #

An obvious use of pathfinding is in sat-navs (or GPS for our friends across the pond), which guide people through maps from their current location to their destination. In this case, nodes could represent junctions or roundabouts, and edges would be the roads. Of course, sat-nav routing is far more complex than this, but it’s likely that some form of pathfinding algorithm is involved.

Implementations #

There are loads of ways to implement pathfinding, but the general idea is to find the shortest path between two nodes. For simplicity’s sake, this post will focus on two key algorithms. They are:

Dijkstra #

Dijkstra’s algorithm is the foundation for almost all pathfinding methods. The basic idea is to find the shortest path to the destination by starting at the source node and moving to a neighbouring node, provided it brings you closer to your goal. This process repeats until the destination is reached.

If you’re using NetworkX, you can implement this in various ways, but the simplest method is to use the following, making sure the method is explicitly set to ‘dijkstra’…

>>> path = nx.shortest_path(G, source, target, method='dijkstra')

A* (A star) #

A* is a variation of Dijkstra’s algorithm, but it’s more commonly used in game development because it’s faster and less complex, as it looks at fewer nodes. The key difference is that A* uses a specific heuristic to better estimate the distance (or cost/weight) between nodes. This could be based on a complex in-game metric or something simpler like the Manhattan or Euclidean distance between two points.

To use A* in NetworkX, you’ll need to define your distance heuristic function. The NetworkX documentation provides a great example of using Euclidean distance to calculate the cost.

>>> path = nx.astar_path(G, source, target, heuristic=dist)

Conclusions #

It’s safe to say that pathfinding is a widely applicable technique and isn’t just confined to network analysis. In this guide, we’ve only skimmed the surface of what pathfinding is all about. There are plenty of great resources out there that go into more depth and explain this topic much better than I can. Honestly, pathfinding isn’t my speciality!

Prev: Subgraphs Next: Visualisation