Core Analysis on Large Networks #

Networks can range from tiny, simple interactions to huge, complex systems. Trying to figure out what’s happening in such a large network can be tricky, right?

Luckily, there’s a handy method to break things down, and it’s called core analysis (also known as degeneracy). This technique simplifies a large network into a more manageable form. One of the most popular ways to do this is by using the k-core algorithm.

Introducing k-core #

The k-core algorithm is the go-to method. It works by peeling off edges from nodes, making sure that every node left in the network has at least k edges (where k is its degree). Basically, the number k tells you the level of the core you’re dealing with.

For example, let’s take a simple directed network of 10 nodes, where edges are created with a probability of 0.25. This will help us visualize how core analysis works in action!

>>> G = nx.fast_gnp_random_graph(n=10, p=0.25, directed=True)

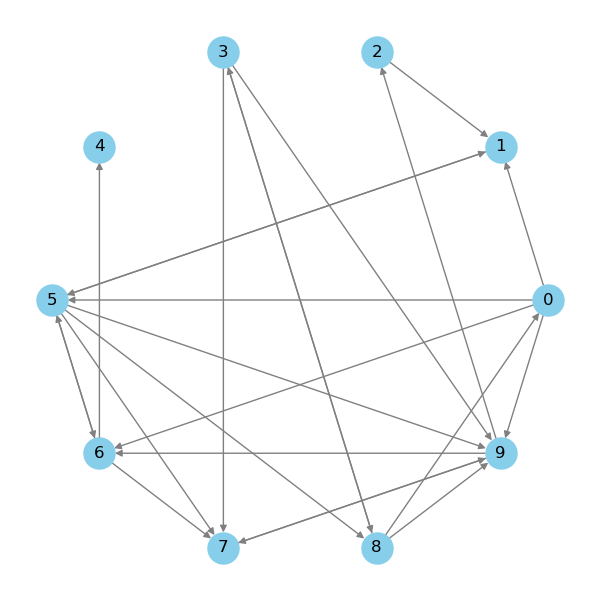
So, as you can see, this gives us a pretty basic network where every node is connected to the others. We can achieve this by making a copy of the original graph G using the copy method and by applying nx.k_core with the value of k provided. When we apply k-core with k= 3, here’s what we get.

>>> Gk = G.copy()
>>> Gk = nx.k_core(G_k, k=3)

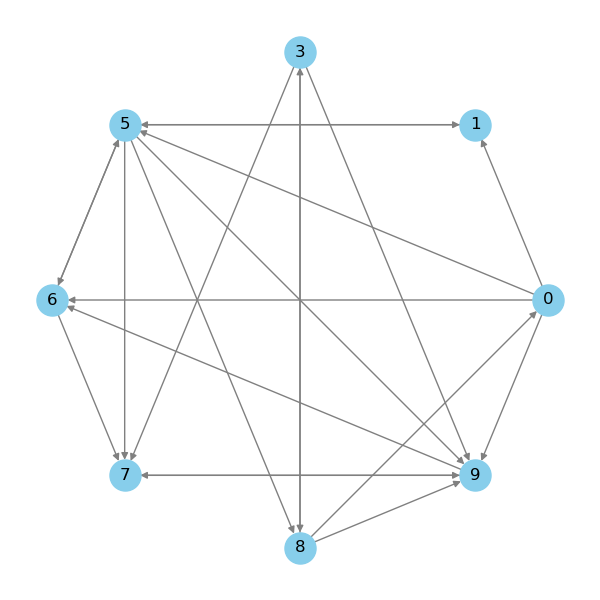
As you can see, a few nodes that were in the original network have now been removed.

Hopefully, you’re starting to get why k-core is a handy way to shrink down the size of a graph. For much bigger graphs, the value of k can get into the hundreds or even thousands.

How is this different from community detection? #

You might be wondering, “Wait, how is this any different from community detection?” “Aren’t they both about finding smaller groups of nodes?” While that’s not wrong, k-core focuses on reducing the graph’s size and identifying the highly connected ‘core’, whereas community detection is more about clustering or grouping nodes.

Here’s a fun way to think about it: imagine k-core like peeling an onion. As you increase the value of k, it’s like peeling away layers until you reach the most centralized and important part at the core.

Other Algorithms #

While k-core is one of the most popular ways to get to the core of a network, there are a few other algorithms worth mentioning.

K-shell #

>>> nx.k_shell(G)

K-shell is similar to k-core, but it’s mainly used for ranking nodes by their degree. The idea is that a network can have “shells” from k = 1 to infinity. For example, k = 1 means nodes with just one edge connected to them. So it’s more about breaking the network down into layers rather than focusing on a single core.

k-crust #

>>> nx.k_crust(G)

With k-crust, instead of looking at the core, you’re actually paying attention to the nodes and edges that get discarded. It gives you what’s left over on the outer parts of the core, aka the ‘crust’.

k-corona #

>>> nx.k_corona(G, k)

No, this has nothing to do with COVID-19, don’t worry 😉.

K-corona is all about finding nodes inside the core that have exactly k connections to their neighboring nodes. It returns all the nodes and edges that match that criteria.

Final Thoughts #

In this quick guide, we covered why k-core analysis is used for large-scale networks and touched on a few other algorithms that build on similar ideas. K-core might not be the easiest concept to explain, but it’s a powerful tool for understanding the key components of densely connected networks.

Prev: Community Detection Next: Subgraphs